§1.8 无穷小的比较

两个无穷小的乘积仍是无穷小，而两个无穷小之商却有如下几种情况：

例如：当时，、、都是无穷小，但是

，，

两个无穷小之比的极限的各种不同情况， 反映出不同无穷小趋向于零时，在“快慢”上是有区别的。

由上述极限，我们粗略地感觉到：较趋向于零更快，而与趋向于零时，在快慢上大体相当。

一、定义

下面的及都是同一个自变量的变化过程中的无穷小， 而也是在这个变化过程中的极限。

如果，就说是比高阶的无穷小，记作；

如果，就说是比低阶的无穷小；

如果，就说是与同阶的无穷小；

如果，就说与是等价无穷小，记作。

据此定义，当时，是比高阶的无穷小，

而与是同阶的无穷小，

由极限，与是等价无穷小。

二、等价无穷小的一个重要性质

证明：

这一性质表明， 求两个无穷小之比的极限，分子及分母都可用等价无穷小来代替，从而达到简化极限的计算之目的。

【例1】求

解：当时， ， 所以

【例2】求

解：令 ， 则 ， 且

于是我们有： 当 时

上述两例使我们看到了等价无穷小代换在求极限时的“威力”，但是，运用这一方法时应该注意以下两点：

【例3】求

解：原式=

= =

注：

如果用等价无穷小代换， 就会得出错误的结论。

， 原式= ==

为了使同学们对这一例子有更深的了解，我们利用计算机程序gs0105.m，可给出函数在区间（0.001, 1）上的图象。

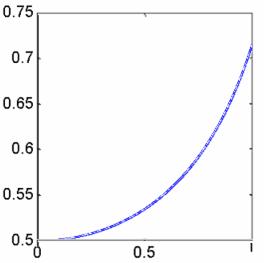
由图象不难看出，在0附近，函数值接近于0.5,而不是0呀！

【例4】求

解： 令 ， 则 ，且

原式= =

=

=

=

注：